Credits

What Will I Learn?
- Definir matrices.
- Operaciones básicas de matrices con números.
- Operaciones básicas entre matrices.
- Producto entre elementos de matrices.
Requirements
- Tener Octave instalado en tu computadora.
Difficulty
- Nivel Básico, pero necesario para los futuros programas que se realizarán.
Tutorial Contents
Comenzaremos realizando el proceso de apertura de nuestro software OCTAVE y luego comenzaremos con la creación de matrices desde la consola.
Paso 1
Primero vamos a crear una matriz siguiendo las reglas de Octave. para crear la matriz debemos colocar entre corchetes [] valores separados por coma o espacio entre paréntesis para rellenar las columnas, con un punto y coma separaremos por fila. veamos un ejemplo de las dos maneras de definir una matriz.
[3 5 1;6 3 5;9 0 1]
[3,5,1;6,3,5;9,0,1]
Veamos el resultado en pantalla luego de definir la matriz '3X3' de las dos formas.

Vemos que obtenemos el mismo resultado, ahora que podemos definir matrices vamos a comenzar a hacer operaciones con ellas.
Paso 2
En este paso, vamos a sumar un numero a una matriz 'M'. Primero vamos a definir una matriz con este nombre y a sumarle un elemento. veamos el siguiente código:
M=[1 2 5;3 2 1;4 8 0]
M+10
Veamos el resultado en pantalla luego de sumar '10' a la matriz 'M'
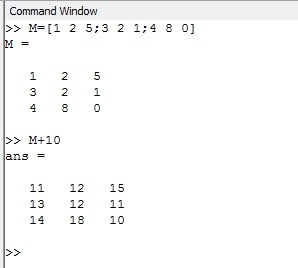
como podemos observar en pantalla el numero '10' se le suma a cada elemento de la matriz.
Paso 3
En este paso vamos a multiplicar ('*') y dividir('/') un numero por la matriz 'M' definida anteriormente. Una ves tengamos la matriz M procedemos hacer lo siguiente:
M=[1 2 5;3 2 1;4 8 0]
M*10
M/10
Veamos el resultado en pantalla:
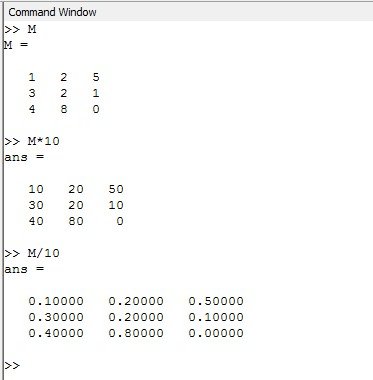
Se observa que cuando multiplicamos o dividimos un numero por una matriz, la operación se va a realizar sobre cada elemento de la matriz. Igualmente para con la suma la resta solo debes tener presente colocar el operador correcto de suma resta multiplicación o división ('+' '-' '*' '/' ) para hacer dicha operación sobre un número.
Paso 4
Es este paso vamos a definir dos matrices 'M' y 'N' , haremos operaciones permitidas entre estas dos matrices. vamos a crear una matriz R que sera el resultado de las operaciones entre M y N.
Comenzaremos con la operación suma '+'. Para sumar dos matrices estas debes ser de igual numero de filas y columnas.
M=[1 2 3;4 5 6;7 8 9]
N=[1 2 3;4 5 6;7 8 9]
R=M+N

Para la operación resta solo debes hacer los siguiente
R=M-N
El resultado de restar la matriz N a la matriz M se muestra en pantalla.
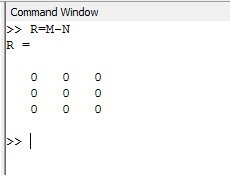
Como los elementos de la matriz M y N son iguales estos se cancelaran y por ellos el resultado es una matriz R de ceros.
Paso 5
La division no esta definida entre matrices por lo que no podemos realizar esta operacion. Entonces vamos a proceder con la multiplicacion entre matrices. Primero vamos a definir dos matrices A y B para multiplicarlas y ver el resultado en la matriz C.
Cuando se multiplican dos matrices, el numero de columnas de la primera matriz debe ser igual al numero de filas de la segunda matriz. El resultado será una matriz con el numero de filas de la primera matriz y el numero de columnas de la segunda matriz. Veamos el ejemplo.
Credits
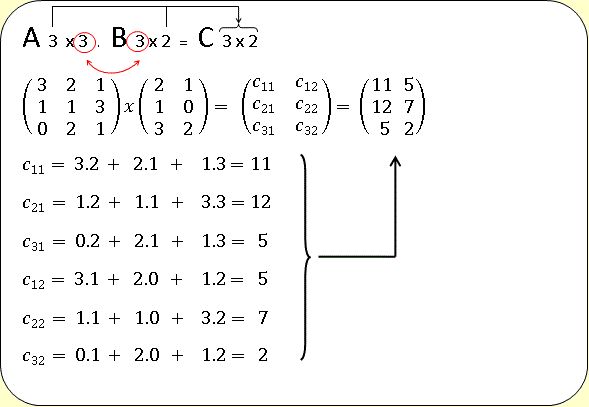
Para replicar el ejemplo definamos las matrices hagamos la multiplicación de A por B y guardemos el resultado en C.
A=[3 2 1;1 1 3;0 2 1]
B=[2 1;1 0;3 2]
C=A*B
Ahora veamos si el resultado coincide con el ejemplo

Podemos observar que el resultado coincide con el ejemplo. La operacion B por A no se puede realizar debido a que el numero de columnas de B(2) es diferente que el numero de filas de A(3).
Paso 6
El producto entre matrices no es conmutativo por lo que es diferente hacer la multiplicación de AB y BA. Vamos a ilustrar con un ejemplo esta desigualdad. Ahora vamos a definir dos matrices con el mismo numero de filas columnas A y B, mostrando el resultado de las operaciones en C
A=[1 2;3 4]
B=[3 4;5 6]
C=AB
C=BA
Mostremos el resultado de C en pantalla para ambos casos.

El resultado muestra que para matrices AB es diferente de BA.
Paso 7
Por ultimo vamos a hacer el producto entre elementos de dos matrices, para ellos las matrices deben ser de las mismas dimensiones.
Con las Matrices anteriormente definidas haremos el producto de elementos de A con B, esto se hace mediante un punto seguido del operador multiplicación, al final mostraremos el resultado en C, también probaremos que este producto es conmutativo.
A=[1 2;3 4]
B=[3 4;5 6]
C=A .* B
C=B .* A
Veamos el resultado de C para ambos casos.

Como observamos en el resultado, el producto usando el punto multiplica cada elemento de la primera matriz por el elemento equivalente en la segundo matriz y el resultado es igual en ambos casos por lo que es conmutativo.
En esta lección se definieron matrices y cómo se realizan operaciones básicas en el programa Octave. En siguientes tutoriales seguiremos trabajando con matrices y vectores, para que en un futuro hagas programas complejos pero primero debes aprender lo esencial.
Curriculum
Posted on Utopian.io - Rewarding Open Source Contributors
Your contribution cannot be approved because it does not refer to or relate to an open-source repository. See here for a definition of "open-source."
This is basic mathematics. It does not provide value to the software.
Further:
End-user focused tutorials must address a minimum of three substantial concepts that are unique to the Open Source project and essential learning requirements for end-users. Preference is given to tutorials that are part of a curriculum (series) of tutorials all of which are sequential and built on previously learned skills and knowledge.
You can contact us on Discord.
[utopian-moderator]
teaching how to use the software gives it a lot of value because more people learn how to use it. and tutorials help people in the learning process. @shreyasgune
The tutorial is very basic. What you are teaching here is Matrix operations. So this is a mathematics lesson NOT a software tutorial. Anyways thanks for the contribution. I hope you can keep this in mind in your future contributions.
Octave is a vector language if you do not know how to use matrices and vectors can not use the software.
wow! great post.. Thanks for your post.. I am getting so much benefit from your kind status.. Keep it up.. always stay with us.. Tell me if you need any kind of help.. I'm always with you.. Best of luck for your future.. Hope you will get a great opportunity from @steemit.. Thank you :) from me @samantha3105 @banjo @cleverbot
Follow me to get free upvote and update
You need a ram upgrade? You should get that checked.
talk to me
I meant talk with me is grammatically incorrect.
Really !!! Thanks for the info then. Are you really a BOT ? You sound human !
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://es.wikipedia.org/wiki/Multiplicaci%C3%B3n_de_matrices