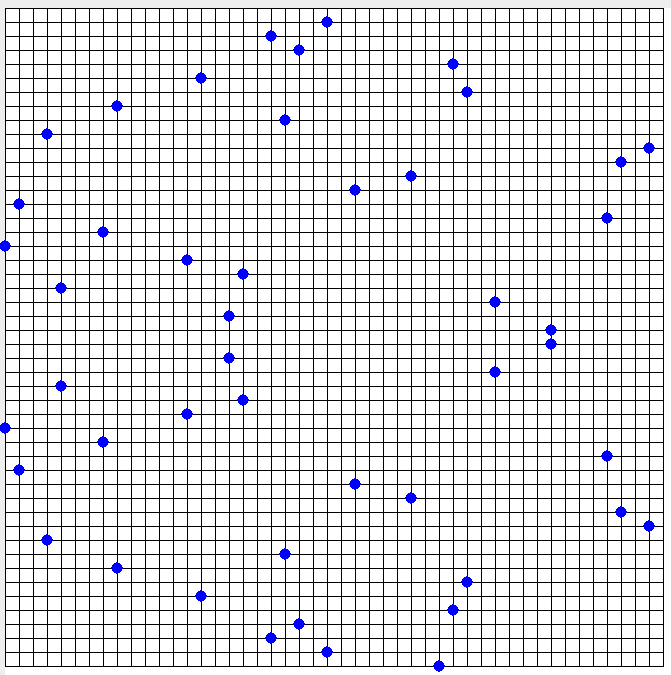
Imagen N° 1 Ejemplo de Curva Elíptica usada para las Firmas ECDSA --- Fuente: Elaboración propia
<div class="text-justify">
<p dir="auto">La Criptografía Asimétrica es la base de la seguridad de muchos sistemas informáticos en la actualidad, el protocolo Bitcoin utiliza la Criptografía de Curva Elíptica (ECDSA) la cual se sustenta en un par de claves, clave privada y clave pública, que básicamente son números, la clave privada corresponde a un número que permite gastar los fondos mientras que la clave pública es un número en base al cual se genera la dirección a la que se envían los fondos. La clave pública puede ser generada a partir de la clave privada de forma fácil mientras que el proceso inverso es imposible de realizar con la potencia computacional existente en la actualidad.
<p dir="auto">El proceso mediante el cual se genera la clave pública a partir de la clave privada se conoce como multiplicación de curva elíptica. En un <a href="https://steemit.com/cervantes/@ydavgonzalez/criptografia-de-curva-eliptica-de-bitcoin-explicada-al-detalle-desentranando-lo-secretos-de-bitcoin" target="_blank" rel="nofollow noreferrer noopener" title="This link will take you away from hive.blog" class="external_link">artículo anterior explique al detalle este proceso de generación de clave privada/clave pública, sin embargo, surge la interrogante <strong>¿cómo se asegura el protocolo Bitcoin de que el usuario que firma una transacción es el propietario de la clave privada sin necesidad de que el propietario tenga que compartir su clave privada?
<p dir="auto">Para explicar este punto primero se hará un repaso de aritmética modular y del proceso de multiplicación de curva elíptica resumiendo lo abordado en un <a href="https://steemit.com/cervantes/@ydavgonzalez/criptografia-de-curva-eliptica-de-bitcoin-explicada-al-detalle-desentranando-lo-secretos-de-bitcoin" target="_blank" rel="nofollow noreferrer noopener" title="This link will take you away from hive.blog" class="external_link">artículo anterior, estos conceptos servirán de base para entender el proceso de firma criptográfica.
<h2>Aritmética Modular o Aritmética de Reloj
<p dir="auto">La aritmética modular consiste en realizar la adición o multiplicación de dos o más números de forma similar a la adición y multiplicación en el conjunto de números enteros y luego calcular el residuo al dividir entre un número entero llamado módulo (denotado por p), por ejemplo:<br />
<code><br />
6 + 10 = 3 (módulo 13) debido a que 6 + 10 = 16 16/13 es 1, y el residuo es 3<br />
9 + 11 = 7 (módulo 13)<br />
8 * 10 = 2 (módulo 13) debido a que 8 * 10 = 80 80/13 es 6 y el residuo es 2<br />
5 * 5 = 4 (módulo 7)<br />
<br />
El conjunto de los enteros módulo p también denotado por F<sub>p consiste en todos los números enteros desde 0 hasta p−1 con las operaciones de adición y multiplicación basadas en la aritmética modular (módulo p) también conocida como “aritmética del reloj”.
<h2>Curvas elípticas en cuerpos de enteros módulo p
<p dir="auto">En general, una curva elíptica en F<sub>p , es una función definida de la siguiente forma<br />
<code><br />
y<sup>2 = x<sup>3+ax+b (módulo p) tal que x,y,a y b pertenecen a F<sub>p<br />
<br />
Cada punto de la curva elíptica satisface la ecuación anterior, en el caso de Bitcoin la curva elíptica usada se define específicamente en el estándar secp256k1 de la siguiente forma:<br />
<code><br />
y<sup>2 = x<sup>3+7 (módulo p)<br />
<br />
Donde p es igual a
<p dir="auto">p = 2<sup>256 - 2<sup>32 - 2<sup>9 - 2<sup>8 - 2<sup>7 - 2<sup>6 - 2<sup>4-1
<p dir="auto">p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
<p dir="auto">Con el objetivo de simplificar los cálculos en el presente artículo se mostrará un ejemplo del proceso de firma criptográfica ECDSA utilizando un valor de p menor (en este caso 23) para comprender los fundamentos matemáticos de esta criptografía.
<p dir="auto">Dados los punto de la curva elíptica<br />
<code><br />
y<sup>2 = x<sup>3+7 (módulo 23)<br />
<br />
Y un punto adicional llamado “punto al infinito” (0,0), el cual no satisface la ecuación de la curva se forma un grupo abeliano, la operación de adición de puntos se define de la siguiente manera:
<p dir="auto">Tres puntos en una curva elíptica están alineados si su suma da cero P<sub>1 + P<sub>2 + P<sub>3 = (0,0), es decir, P<sub>1 + P<sub>2 = - P<sub>3 donde - P<sub>3 corresponde al punto simétrico a P<sub>3, adicionalmente se puede decir que tres punto en F<sub>p están alineados si existe una línea recta que los una, sin embargo, las líneas rectas en F<sub>p no son iguales a las líneas rectas en los números reales.
<p dir="auto">Una línea recta en F<sub>p es el conjunto de puntos (x,y) que satisfacen la ecuación<br />
<code><br />
y = ax + b (módulo p)<br />
<br />
Que es la misma ecuación para los números reales pero aplicando aritmética modular, por ejemplo en F<sub>23 los puntos (1,10) y (6,4) están alineados en la recta<br />
<code><br />
y = 8x+2 (módulo 23)<br />
<br />
Probando con los otros puntos de F<sub>23 se demuestra que el tercer punto alineado en dicha recta es (11,21), por lo tanto el resultado de la adición es el simétrico de (11,21), es decir, (11,2) en caso de que se sume un punto P<sub>1 con el mismo, como no puede trazarse una línea recta entre ambos puntos, la línea recta se extiende para ser la tangente sobre la curva en P<sub>1, esta tangente intersectará a la curva en un punto, el simétrico de dicho punto es el resultado de la adición.
<p dir="auto">Propiedades de la adición de puntos<br />
<code><br />
P<sub>1 + 0 = 0 + P<sub>1 = P<sub>1<br />
P<sub>1 + ( - P<sub><sub>1) = 0 un punto más su simétrico es igual al punto al infinito<br />
<br />
Las ecuaciones para calcular la suma de dos puntos son las siguientes, dados P<sub>1 = (x<sub>1, y<sub>1) y P<sub>2=(x<sub>2,y<sub>2) su suma es igual a P<sub>3 =(x<sub>3,y<sub>3)<br />
<code><br />
x<sub>3 = m<sup>2 - x<sub>1 - x<sub>2 (módulo p)<br />
y<sub>3 = m * (x<sub>1 - x<sub>3 ) - y<sub>1 (módulo p)<br />
<br />
Donde<br />
<code><br />
m = (y<sub>2 - y<sub>1 ) * (x<sub>2 - x<sub>1)<sup>-1 (módulo p) si P<sub>1 ≠ P<sub>2<br />
m = (3 * x<sub>1<sup>2 ) * (2 * y<sub>1)<sup>-1 ( módulo p) si P<sub>1 = P<sub>2<br />
<br />
La demostración del porque se usan estas formula escapa al alcance de este artículo. Ahora se define la multiplicación escalar dentro de la curva elíptica de la siguiente forma<br />
<code><br />
n * P<sub>1 = (P<sub>1 + P<sub>1 + ⋯ + P<sub>1) n veces<br />
<br />
Donde n es un número entero menor que p, por ejemplo en F<sub>23 si se define la curva elíptica y<sup>2 = x<sup>3+7 (módulo 23) se obtendría la siguiente representación gráfica
<div class="text-center">
<p dir="auto"><img src="https://images.hive.blog/768x0/https://steemitimages.com/DQmT8vpdv2bcKbhds2znGCY2CSD6PbdrqvdxeHMmFHfmgRv/F23.png" alt="F23.png" srcset="https://images.hive.blog/768x0/https://steemitimages.com/DQmT8vpdv2bcKbhds2znGCY2CSD6PbdrqvdxeHMmFHfmgRv/F23.png 1x, https://images.hive.blog/1536x0/https://steemitimages.com/DQmT8vpdv2bcKbhds2znGCY2CSD6PbdrqvdxeHMmFHfmgRv/F23.png 2x" /><br />
<strong>Imagen N° 2 Curva Elíptica y<sup>2 = x<sup>3+7 (módulo 23) en F<sub>23 --- Fuente: Elaboración propia
<p dir="auto">Luego si en la curva anterior se define el punto P<sub>1 = (1,10) como punto de partida y se multiplica dicho punto por un escalar n se obtendrían los siguientes puntos dependiendo del valor de n
<div class="text-center">
<p dir="auto"><img src="https://images.hive.blog/768x0/https://steemitimages.com/DQmT9xSZ51P33SvRCwcnSHPRfAyrr94PzACDoxZ9nQNnfsj/tab1.png" alt="tab1.png" srcset="https://images.hive.blog/768x0/https://steemitimages.com/DQmT9xSZ51P33SvRCwcnSHPRfAyrr94PzACDoxZ9nQNnfsj/tab1.png 1x, https://images.hive.blog/1536x0/https://steemitimages.com/DQmT9xSZ51P33SvRCwcnSHPRfAyrr94PzACDoxZ9nQNnfsj/tab1.png 2x" /><br />
<strong>Tabla N° 1 Puntos de la Curva Elíptica y<sup>2 = x<sup>3+7 (módulo 23) en F<sub>23 --- Fuente: Elaboración propia
<p dir="auto">Como se puede observar al multiplicar por diferentes valores escalares tomando (1,10) como punto generador se obtiene un subgrupo cíclico compuesto por 24 elementos que se repiten continuamente.
<p dir="auto">En el caso de la curva elíptica de bitcoin el punto generador G es el siguiente<br />
<code><br />
X=55066263022277343669578718895168534326250603453777594175500187360389116729240<br />
Y=32670510020758816978083085130507043184471273380659243275938904335757337482424<br />
<br />
El punto obtenido al multiplicar el punto generador G por la clave privada es la clave pública la cual se suele representar en dos formatos diferentes, comprimida y descomprimida.
<p dir="auto">A continuación se presenta un ejemplo de la firma criptográfica ECDSA para la curva mostrada anteriormente.<br />
<code><br />
y<sup>2 = x<sup>3+7 (módulo 23)<br />
<br />
La cual es la misma curva con la que trabaja el protocolo de Bitcoin pero cambiando el valor del módulo para simplificar los cálculos, en la curva anterior si se selecciona el número d=20 como clave privada se puede apreciar en la tabla N° 1 que la clave pública correspondiente sería el punto Q = (11,21).
<h2>Proceso de Firma Criptográfica ECDSA
<p dir="auto">1- Se selecciona el mensaje a firmar M en el caso de Bitcoin se corresponde al SHA-256 de cierta información de la transacción en formato hexadecimal, la Curva Elíptica E de orden n (el orden es el número de puntos) y el punto Generador G.
<p dir="auto">En este artículo se usará como ejemplo de mensaje el número 17, la curva elíptica<br />
<code><br />
y<sup>2 = x<sup>3+7 (módulo 23)<br />
<br />
El punto generador será G= (1,10) esta curva posee 24 puntos por lo tanto su orden es n=24
<p dir="auto">2- Se selecciona un número aleatorio k entre 1 y n, por ejemplo el número 13.
<p dir="auto">3- Se calcula k * G, obteniéndose el punto (x<sub>1,y<sub>1), en este caso sería<br />
<code><br />
13 * (1,10) = (16,3) ver Tabla N°1<br />
<br />
4- Se calcula R = x<sub>1 mod n, si R = 0 se regresa al primer paso (x<sub>1 es tratado como un entero en aritmética modular)<br />
<code><br />
R = 16 mod 24 = 16<br />
<br />
5- Se calcula k<sup>-1 mod n (mediante el Algoritmo de Euclides Extendido) en este caso<br />
<code><br />
13 mod 24 = 13 lo cual es cierto debido a que 13 * 13 = 1 (mod 24)<br />
<br />
6- Se calcula S = k<sup>-1 * ( M + d * R) mod n si S = 0 regresar al primer paso<br />
<code><br />
S = 13 * (17 + 20 * 16) (mod 24)<br />
S = 13 * 1 (mod 24)<br />
S = 13<br />
<br />
7- La firma del mensaje son los números (R, S).<br />
<code><br />
(16,13)<br />
<h2>Proceso de verificación de la Firma Criptográfica ECDSA
<p dir="auto">El proceso de verificación de la firma se realiza de la siguiente manera
<p dir="auto">1- Se verifica que R y S estén entre 1 y n-1<br />
<code><br />
16 y 13 son menores que 24, por lo tanto el paso 1 se cumple<br />
<br />
2- Se calcula W = S<sup>-1 (mod n)<br />
<code><br />
W = 13<sup>-1 (mod 24)<br />
W = 13 lo cual es cierto debido a que 13 * 13 = 1 (mod 24)<br />
<br />
3- Se calcula U<sub>1 = M * W (mod n)<br />
<code><br />
U<sub>1 = 17 * 13 (mod 24) = 5<br />
<br />
4- Se calcula U<sub>2= R * W (mod n)<br />
<code><br />
U<sub>2 = 16 * 13 (mod 24) = 16<br />
<br />
5- Se calcula el punto U<sub>1 * G + U<sub>2 * Q = (x0,y0)<br />
<code><br />
5 * G + 16 * Q = (19,9) + 16 * (11,21)<br />
(19,9) + (4,18)<br />
(16,3)<br />
<br />
6- Se calcula V = x<sub>0 mod n<br />
<code><br />
V = 16 mod 24 = 16<br />
<br />
7- La firma verifica si y solo si V = R, lo cual se cumple debido a que<br />
<code><br />
16 = 16<br />
<p dir="auto">Por lo tanto la firma criptografica ECDSA del mensaje es válida, se puede apreciar que la firma pudo ser verificada sin necesidad de dar a conocer la clave privada, solamente con la clave pública.


Con este post nos muestras las matemáticas ocultas detrás del Bitcoin, una información que es importante tener presente si queremos adentrarnos de lleno en el mundo de las Criptomonedas. Gracias por compartir!
Gracias por el apoyo.
Gracias a ti por tus valiosos aportes en cuanto a matemáticas aplicadas a diversos temas de interés.
todos los días de aprende algo nuevo muy interesante tu post @ydavgonzalez
Muchas gracias, Saludos.
Saludos @ydavgonzalez, excelente publicación. Una pregunta: si deseo iniciarme en el estudio a profundidad de las matemáticas en las que se sustenta el mundo de las criptomonedas, ¿con que me recomendarías comenzar?
El libro Mastering in Bitcoin presenta una introducción bastante sencilla a este tema.
Muy bien estructurado tu articulo. Definitivamente conoces y manejas muy bien tu campo. Felicidades.
Gracias por el apoyo.
Hi! I am a robot. I just upvoted you! Readers might be interested in similar content by the same author:
https://steemit.com/cervantes/@ydavgonzalez/criptografia-de-curva-eliptica-de-bitcoin-explicada-al-detalle-desentranando-lo-secretos-de-bitcoin
The article that indicates is my previous article that can serve as an introduction to this post.
El artículo que indica es mi artículo previo que sirve como introducción a este post.
Muy bueno tu artículo.
¡Excelente artículo!