Cuando nos dedicamos a seleccionar a un grupo de sucesos, individuos, cualidades o elementos que tengan alguna particularidad en común, los podemos "meter en un mismo saco" (coloquialmente), es decir, podemos agruparlos en un conjunto (matemáticamente). Al conjunto por extensión o por comprensión los representamos por medio de símbolos gráficos (cajas o círculos, también entre caracteres alfanuméricos especiales (corchetes, paréntesis o llaves), siendo susceptibles a la aplicación de las propiedades de conjuntos: unión e intersección de conjuntos.

Nuevamente, debemos tener presente los términos matemáticos relacionados con las probabilidades, a) el espacio muestral, como el total de los elementos que cumplen ciertas condiciones características que formarían un conjunto universal que daría lugar a las posibilidades que ocurra un evento particular, b) la regla de Laplace, para calcular el porcentaje de probabilidad dentro de un número finito de experimentos aleatorios.
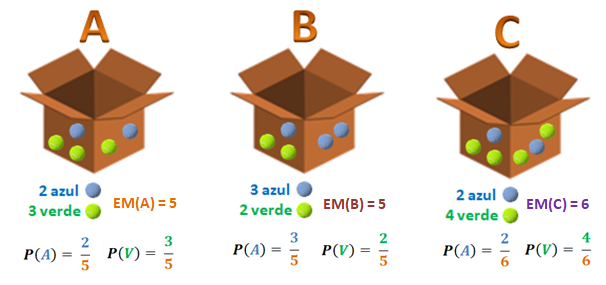
Vamos a dilucidar estos aspectos básicos mediante un ejemplo particular. Supongamos que se tienen 2 grupos de esferas de colores, 7 esferas son de color azul y 9 esferas son de color verde. Se toman 3 cajas de cartón y se etiquetan con las letras A, B y C para ingresar varias esferas de colores. Se forman 3 conjuntos con los elementos señalados:
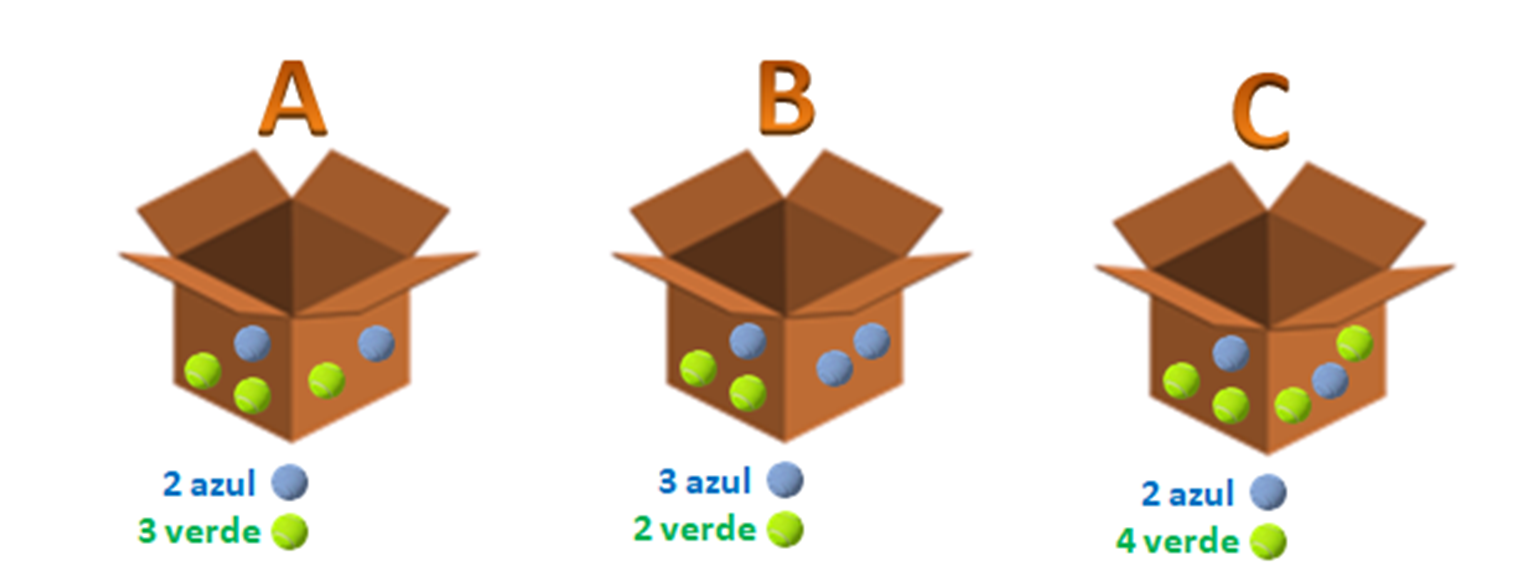
Si se extrae 1 esfera al azar desde cada caja, ¿cuál es la probabilidad de sacar 2 esferas de color azul y 1 esfera verde?
Note que se han formado 3 conjuntos (A, B y C) con elementos comunes (esferas de color azul y verde), por lo que la lógica matemática nos indica que se originaría una intersección de conjuntos con eventos probabilísticos de sacar 1 esfera de color azul o verde de cada una de las cajas, dada como: A⋂B⋂C.
La regla multiplicativa que involucra a los eventos independientes se puede representar mediante la relación general:
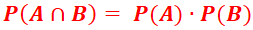
Repetimos lo que expliqué en publicaciones anteriores, la probabilidad de ocurrencia de un evento se determina mediante la Regla de Laplace:


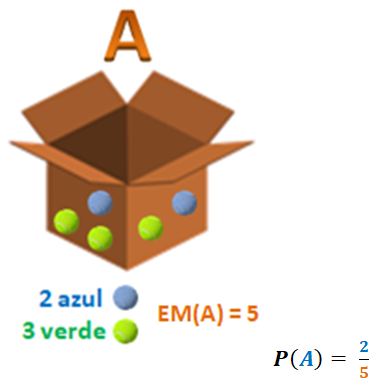
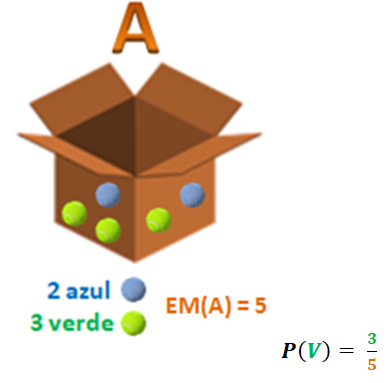
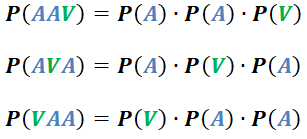
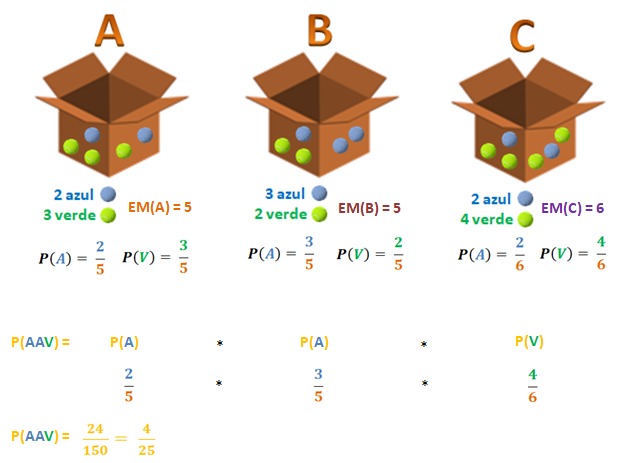
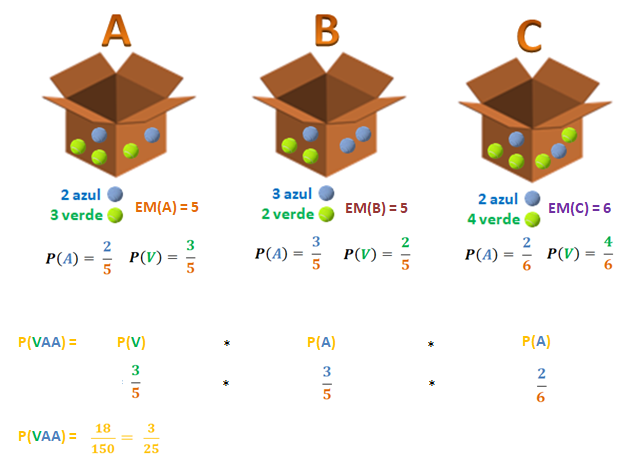
¡Mucha atención!: porque este no es el reultado final, pues se trata de sólo 1 de las posibilidades entre las 3 que hemos planteado, así que sigamos desarrollando este interesante ejemplo.
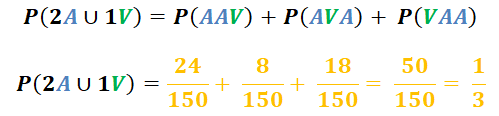
Apoyo bibliográfico y fuente de imágenes
Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:
- Imagen de geralt: Unión e intersección de conjuntos
- Video: Probabilidad y Estadística
- Presentación: Probabilidad
- Blog: Probabilidad de la unión e intersección de sucesos
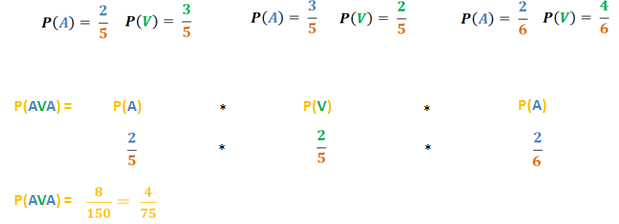
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Congratulations your publication has been chosen among the best of the day.
KEEP CREATING GOOD CONTENT.