

Introducción a la teoría de conjuntos y su notación
La noción de conjunto es una idea básica y natural en Matemáticas. La la teoría de conjuntos descrita de manera rigurosa es una tarea mucho más compleja de lo que se intentaremos mostrar aquí. Para comenzar, todos aceptaremos y asumiremos que tenemos una idea más o menos clara de lo que es un conjunto de objetos o de elementos. Por ejemplo, podemos dar algunos conjuntos que nuestra mente puede fácilmente identificar, a saber:
- el conjunto de los números enteros,
- el conjunto de los números pares,
- el conjunto de los puntos de una recta,
- el conjunto de las rectas de un plano
- el conjunto de ...
así comienza a volar nuestra mente y crear conjuntos de todos los objetos que se nos puedan ocurrir, haga el intento y verá todo lo que se puede clasificar como conjunto.
Desde la escuela básica y la escuela secundaria se ha desarrollado este lenguaje y lo utilizaremos sin más definiciones.


 es un elemento del conjunto
es un elemento del conjunto  , escribiremos
, escribiremos  . Para decir que
. Para decir que  no está en
no está en  , escribiremos
, escribiremos  .
.
Aceptaremos que existe un conjunto llamado vacío, que no tiene elemento alguno y lo vamos a denotar con el símbolo  .
.
- El conjunto de las rectas del plano que pasan por un punto fijo P, esta contenido en el conjunto de todas las rectas del plano.
- El conjunto de todos los números enteros múltiplos de 4, es un subconjunto del conjunto de los números pares.
- La colección de todos los capítulos de un libro, es un ejemplo de un conjunto.
Operaciones o Álgebra de conjuntos
Si A y B son dos conjuntos, se pueden crear nuevos conjuntos a partir de ellos mediante operaciones elementales.
- El conjunto intersección: La intersección de A y B es el conjunto de todos los elementos que pertenecen a A y a B
Imagen elaborada por @abdulmath, diseñadas y editada con GIMP.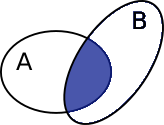
 .
En otras palabras, escrito de manera formal, tenemos:
.
En otras palabras, escrito de manera formal, tenemos:  . Si la intersección de dos conjuntos es vacía, es decir,
. Si la intersección de dos conjuntos es vacía, es decir,  , se dice que los conjuntos son disjuntos.
, se dice que los conjuntos son disjuntos. - El conjunto Unión: La unión de dos conjuntos A y B es el conjunto formado por todos los elementos que están en A ó en B
Imagen elaborada por @abdulmath, diseñadas y editada con GIMP.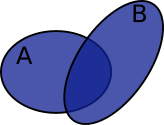
 .
En otras palabras, escrito de manera formal, tenemos:
.
En otras palabras, escrito de manera formal, tenemos: 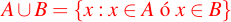
- El conjunto Diferencia: La diferencia del conjunto A menos el conjunto B es el conjunto formado por todos los elementos de A que no están en B
Imagen elaborada por @abdulmath, diseñadas y editada con GIMP.
 .
En otras palabras, escrito de manera formal, tenemos:
.
En otras palabras, escrito de manera formal, tenemos: 
- El conjunto universal o universo: Como conjunto universal vamos a denotar a un conjunto E especial, el cual contiene todos los elementos que se desean considerar en el problema, o tema, sin pretender contener todo lo que no es de interés al problema del cual estemos hablando. Este conjunto universal se supone conocido en cada problema y del cual se pueden seleccionar elementos para construir subconjuntos.
- El conjunto Complemento: Digamos que tenemos un conjunto universal E. Cualquier conjunto A que se considere será un subconjunto de EA
Imagen elaborada por @abdulmath, diseñadas y editada con GIMP.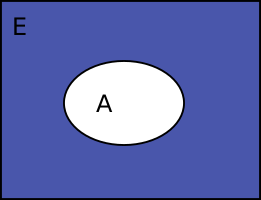
 . Así, la diferencia
. Así, la diferencia  se llamará el complemento de y se denotará por
se llamará el complemento de y se denotará por 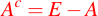 .
En otras palabras, escrito de manera formal, tenemos:
.
En otras palabras, escrito de manera formal, tenemos: 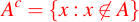
Propiedades de las operaciones con conjuntos
Las operaciones con conjuntos, gozan de algunas propiedades de fácil comprobación las cuales vamos a enunciar, a saber:
- La unión y la intersección son conmutativas
Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.
y GIMP.

- La unión y la intersección son asociativas
Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.
y GIMP.

- La unión es distributiva con respecto a la intersección
Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.
y GIMP.

- La intersección es distributiva con respecto a la unión
Imagen elaborada por @abdulmath, diseñadas y editada con y GIMP.
y GIMP.


Queridos amigos y lectores, espero hayan disfrutado leyendo y estudiando esta publicación, los espero en una próxima entrega donde seguiré tratando algunos temas de matemáticas, para así, además de compartir con ustedes mi experiencia, pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco mas del maravilloso mundo de las matemáticas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias.
- Devlin, Keith. Sets, functions, and logic: an introduction to abstract mathematics. CRC Press, 2003.
- Lipschutz, Seymour. Teoría de conjuntos y temas afines. McGraw-Hill. 1991.
También los invito a leer mis otras publicaciones que puedan ser de su interés:
- El triángulo de Pascal y los productos notables.
- Resolución de Ecuaciones e Inecuaciones lineales de 1er orden con una incógnita.
- Resolución de una ecuación de 2do grado con una incógnita.
- Otras consideraciones de la ecuación de 2do grado con una incógnita.
- Resolución de inecuaciones de 2do grado con una incógnita en el conjunto de los números reales.
- Sistema de dos ecuaciones de 1er grado con dos incógnitas
Todas las imágenes son propias, creadas y editadas con software libre:  , Karbon, Inkscape y GIMP.
, Karbon, Inkscape y GIMP.
Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.

Felicitaciones por tan estupenda publicación y por compartir contenido que deja aprendizaje para la comunidad. Te dejo un abrazo y bendiciones.
Buena vibra.
Muchas gracias por tus comentarios, agradecido. Saludos y un beso.
que hay como esta todo
Hola @duque, todo bien gracias. Gracias por visitarme y leerme. Saludos y un abrazo.
Hi @abdulmath!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Saludos @abdulmath
Hola @gabybarboza, que bueno verte nuevamente por acá. Saludos y un abrazo.