
Steemados amigos, acá les traigo esta nueva publicación, dedicada a las matemáticas. La motivación que me llevo a escribir sobre ella, fue debido a que durante la clase que dictaba a mis estudiantes de Matematicas I, se presentó una situación que para mi, es de absoluta incredulidad. Las cual les relato y luego paso a hablar un poco del tema en cuestión.
En medio de la clase, cuando estabamos resolviendo algunos problemas de integración, en medio de la explicación se levanta uno de los estudiantes y me pregunta: Profesor como hizo para que esa suma elevada al cuadrado le quedará así?
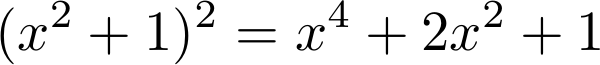
para lo que le conteste pues desarrollen el producto notable, y todos contestaron okey profesor (pero muy intuición de profesor, jajajaja, pues todos quedaron con la cara de no haber entendido nada), les pregunte: ¿acaso a ustedes su profesor de matemáticas básicas no les enseño como desarrollar productos notables? A lo que contestaron: no, la profesora siempre estaba enferma y nunca nos dio clase, solo una semana al principio y otra al final del semestre.


Ellos dijeron: profesor es que nos daba pena decirle eso.
Entonces para no entrar en detalles, les dije, les voy a enseñar como desarrollar productos notables, y será de una forma que más nunca se les olvidará, les voy a enseñar como se usa el triángulo de Pascal para desarrollar productos notables.
Quien es Blaise Pascal
Blaise Pascal fué un matematico, físico, filósofo y escritor francés, nació en Auvernia, una región que pertenecía al centro de Francia el 19 de junio 1623, y murió el 19 de agosto de 1662, en Paris, Francia. Entres las contribuciones mas importantes en las matemáticas, podemos nombrar, el teorema de Pascal, su aporte al diseño y construcción de calculadoras mecánicas, el Traité du triangle arithmétique (teoría de probabilidad y combinatoria).Traité du triangle arithmétique (Tratado del triángulo aritmético)
El Traité du triangle arithmétique traducido, el Tratado del triángulo aritmético, fue publicado en el año 1654 por Blaise Pascal, donde reúne varios resultados importantes para las matemáticas y sus aplicaciones a otras ciencias, entre los que destacan las aplicaciones de la teoría combinatoria a la teoría de las probabilidades y todas sus implicaciones. El dicho tratado muestra 19 propiedades deducidas a partir de la definición de combinatoria. Muchas de estas definiciones ya se conocían de antes, pero no se tenia una demostración formal de las mismas. Una de las técnicas usadas por Pascal para la demostración de estas propiedades fue a partir de un proceso inductivo, que conocemos en matemática, como inducción matemática.Construcción del Triángulo de Pascal
La construcción del triángulo de Pascal, se hace de manera algorítmica, siguiendo un modelo que empieza con un 1 en la parte superior del triangulo, hasta el infinito en forma de árbol.
El mismo lo vamos a construir con filas y en cada fila agregaremos nodos, que no son más que los números de los que esta compuesto el triángulo.
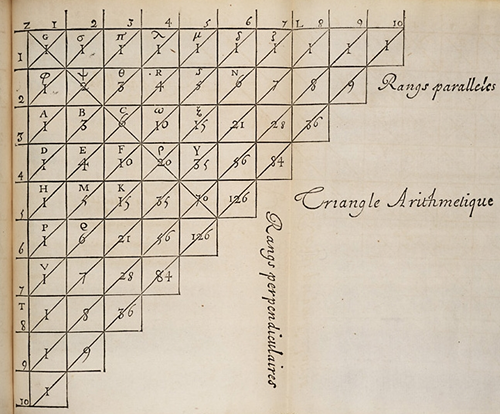
En la figura que vemos anexa podemos observar la versión del triángulo de Pascal, construida y escrita por el mismo Blaise Pascal, en su Tratado del triángulo aritmético.
Comenzamos con la construcción sin justificar ni hablar mucho de su porque, solo de como podemos construirlo manualmente y podemos usarlo posteriormente para desarrollos de productos notables.
Lo primero que agregamos es una fila con un 1 y una segunda fila con un parte de 1's, como vemos a continuación:
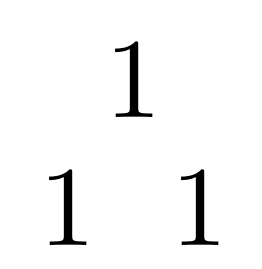
Posteriormente agregamos otra fila compuesta por 3 nodos y los valores 1, 2, 1 respectivamente, como vemos a continuación:
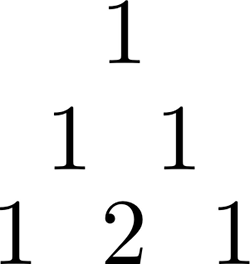
Se preguntaran como obtuve esa fila, o será que la invente o coloque al azar? Pues no, la forma de obtener esta nueva fila y cualquiera posteriormente es siguiendo un proceso algorítmico que podemos definir de la siguiente manera:
- Cada nueva fila tendrán un nodo más que la fila anterior.
- Cada fila comienza con un 1 y termina con un 1.
- Los nodos internos los obtenemos como suma de los del términos adyacentes en la fila superior.
Siguiendo estas tres premisas, podemos ver claramente que el 2 de la tercera fila lo obtuvimos como la suma de los términos adyacentes en la fila superior que es 1+1=2. Así, si seguimos al agregar una nueva fila a nuestro triángulo, tenemos que agregar un nuevo nodo por lo tanto la fila esta compuesta por 4 nodos a saber, 1, 3, 3, 1 y obtenemos lo siguiente:
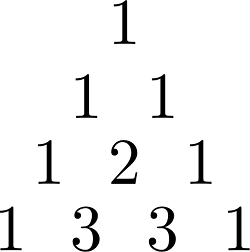
Hagamos un par de filas más y veamos lo que sucede, si agregamos una fila más al triángulo anterior tendría una fila de 5 nodos, a saber, 1, 4, 6, 4, 1. Y si agregamos otra fila con 6 nodos ahora, tenemos los siguientes números, 1, 5, 10, 10, 5, 1, como podemos ver en la figura siguiente:

Bien ya que aprendimos a construir el triángulo de Pascal, ¿como lo usamos para el desarrollo de productos notables?
Triangulo de Pascal y su relación con los desarrollos de productos notables
El triángulo de Pascal nos indica los coeficientes del desarrollo de productos notables, como sigue:

Es decir,
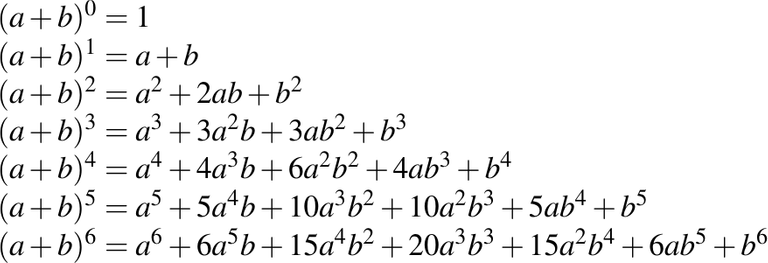
El triángulo de Pascal tiene otras aplicaciones quizás más importantes dentro de las matemáticas, pero mi intención era mostrar solo una pequeña parte de como usarlo para el desarrollo de los productos notables. Espero sus comentarios y votos sobre esta publicación y pueden visitar mi blog y ver mis otras publicaciones y las próximas que estaré realizando en los días venideros. Saludos y un abrazo para todos.
Todas las imágenes que no tienen referencia, son propias, editadas con GIMP.


Buena vibra.Hola @abdulmath muy buen artículo y me gusta mucho la diagramación. Felicitaciones.
Gracias, cada día, tratando de hacer las cosas bien y mejor. Saludos y besos
Debo admitir que he sido de las que simplemente me aprendo la formula sin curiosear de donde se origina!! Gracias!! ;);)
Bueno por lo menos, ya sabes de donde salen algunas. jejejejeje. Saludos
Hola @abdulmath seria importante que revisaras los siguientes artículos https://steemit.com/stem-espanol/@carloserp-2000/stem-espanol-reporte-semanal-17 y https://steemit.com/stem-espanol/@carloserp-2000/directrices-sobre-normas-de-derechos-de-autor-en-steemstem-stem-espanol
Leí tus artículos, me puede indicar cual fue el problema que encontraste? Gracias.
POR FIN!!! hasta ahora lo entiendo... por qué no me lo explicaste antes... así es muy fácil... Algo que me llama mucho la atención de Pascal como filósofo escolástico es su posición frente a la duda de la existencia o no de Dios, porque es diametralmente opuesta a la mia jajajaja... muchas gracias hermano... un fuerte abrazo
Hola, que bueno que ya lo entendieras, jejejejeje pues si todos los profesores pusieran el empeño en aclarar las dudas como debe ser, o cumplir con los programas de las materias, te aseguro que tendríamos mejores profesionales. Saludos y gracias por leer mi publicación. Un abrazo.