"Hello? qed, speaking."
"Dude, hi, you gotta help me out. But we gonna do it quick, my phone battery is dying."
"Man, it's 8 in the morning. What's up?"
"I'm in a art histoy exam, and I'm struggling with the last question. It's really easy but I'm brain dead now."
"Okay, no problem. Shoot."
"So there's this picture. You know. The woman who is smiling. What's the name of the picture, I forgot."

"A picture of a woman smiling, huh? Can you be more precise?"
"You know, this picture. It's old. Famous smiling woman."
"Marilyn Monroe?"
"No, it's a painting."
"Well I'm not so good with classical art, I gotta admit."
"No, you know the picture."
"Make me the picture of it that you make with your phone, how about that?"
"I can't. The Prof would see it. I can only describe it."
"Well, you suck at describing."
"Let me send you that picture in a classical analog fashion, then."
"Huh?"
"I'm gonna split the frame into 200 pixels and describe you each pixel by seeding you a text."

"A rough scale bitmap scheme? But that's a lot of colors."

"The test will be over before you type out all the 200 color codes."
"Na, scratch that. You don't need a full color picture to know the picture. I'll reduce it to four colors"
"What are the colors?"
"So the sliced picture I'll send you will be 200 pixels, and roughly 1/2 of it is black. Another 1/4 of it is light gray. About 1/8 is dark gray and the remaining 1/8 is white. That's mostly the skin."

"Okay, that simplifies it. So how about this encoding: You go through all 200 pixels, row by row, and for black, you send the sequence '00'. For a light gray pixel, you send the sequence '10'. For dark gray you send '01' and for white you send '11'. So you send me a sequence of 400 digits and then I can reconstruct the picture here and tell you what it is. So for example, '001110'... means 'black, white, light gray,...' and so on."
"Good idea, but we can improve on that."
"Improve how?"
"You chose your symbol chains unwisely. You take two digits per pixel, but you can transmit the information more efficiently."
"How do you know?"
"Just compute the entropy."
"Huh?"
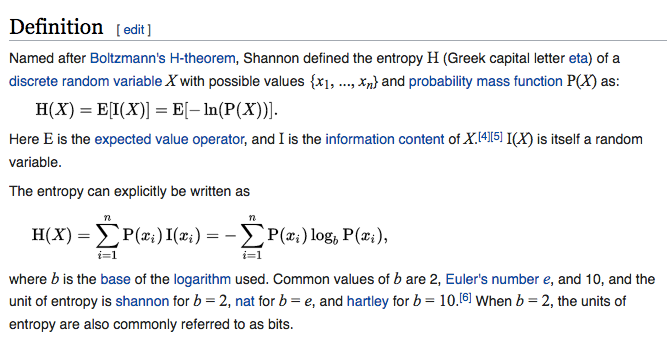
"Well..."
"What the heck are you talking about?"
This makes for an entropy of 7/4, or 1.75.
"What?"
"Well let's try this: Black makes up half of the picture, so encode it with only one digit. For black, I send 0."
"And the other ones?"
"Well, if I send you a '1', you know another color started. If I send '11', you'll know it's white and the color is over. If I send '1' followed by a '0', you'll know the color is not over yet. We make '101' light gray and '100' dark gray."
"So black gets one digit, and the rarer two colors get three."
Exactly. Let's see how many digits we must send this way. There are 200/2 or 100 black pixes. So 100 one digit transmission. There are 200/4 or 50 light gray ones for the two digit case, making for 100 transmission of for color. And finally, there two times 200/8 or 50 for the longer transmissions, making for another 150 in total.
"So 100 + 100 + 150 or 350 digit transmissions total. We don't need 400 anymore with your encoding."
Yes, and since the average transmission length is 350/200 or 1.75 exactly equals the entropy, I know for sure that this is as good as it gets.
"Aha!"
Cute, right?
"Yeah, cute, smartass. Let's get sending so you pass that test..."
Take care
@qed
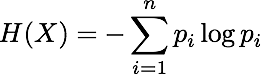
Cool way of writing!