Hi, Good Morning my fellow Steamians. Today, I am going to share on how to find the GCF (Greatest Common Factor) of the bigger number using the Euclidean Algorithm.
So, Let's get started...
Before were going to find the GCF of the number, let me share you steps. After that I am going to give you an example (smaller number to bigger number).
Steps
- You'll be given a 2 numbers and ask you to find the GCF of the two number. Pick the number which is the bigger value.
- Write the number that you pick in the left side and put an equal sign and then write the remaining number in the right side of the equal sign.
- Let's assume that the number in the left side is the product of the two number which is the remaining number and another number which we don't know plus a number which we don't know as our remainder. Let say, the number on the left side let's say m, for the remaining number p, for the unknown number q and for remainder r. So it will look like this:
m = (p)(q) + r- Find the value of the unknown number and the remainder.
- If you already get the value of the unknown number and the remainder, you can observe that we back in this form m = (p)(q) + r, so we will repeat the process to find the q and r until we will get 0 as our remainder.
- If we already achieve 0 as our remainder then look back to the previous remainder since that would be your GCF.
ExamplesGCF (48, 42)
Solution
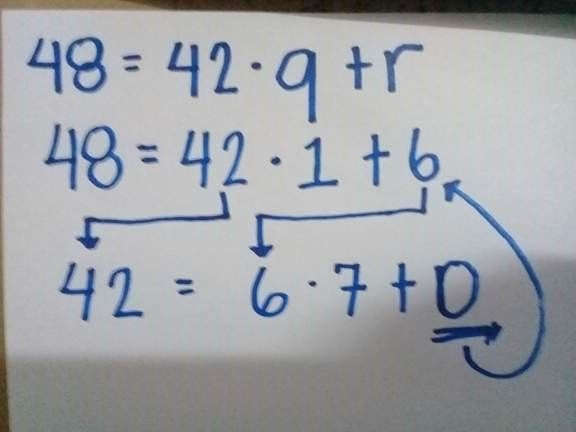
Therefore, the GCF of 48 and 42 is 6.GCF ( 245, 476)
Solution

Therefore, the GCF of 245 and 476 is 7.GCF (4214, 882)
Solution
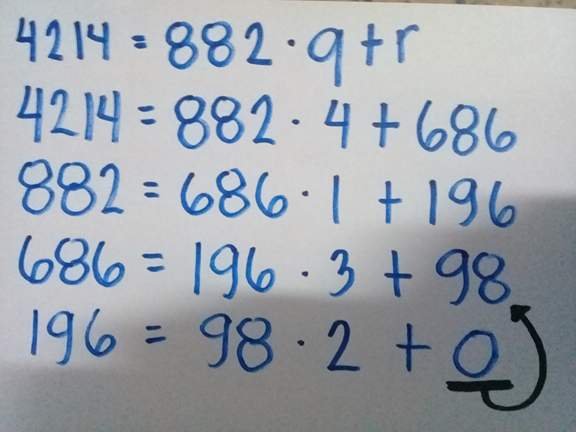
Therefore, the GCF of 4214 and 882 is 98.
There are many ways how to find the GCF of the number and one of these is using Euclidean Algorithm. For me, this is the easiest way to get the GCF of the 2 numbers. If you are interested in math, you can try this techniques in your study if you are a student. Thank you for reading this and feel free to comment. :D
Wow jhernel!
hahaha naa na sa number theory dba? hahaha ge pang post ra nako akong ge tun.an ahahaha 2 birds in 1 stone
:D
@steemiteducation will love this. They have a tag too #steemiteducation. Keep it up! I think an intro post will connect more people to you!
Hi @surpassinggoogle. Thank you for your advice. As a newbie here in this community, it really helps me since I don't know everything about steemit.
I hope you will leave a comment there so that I can have a reference on how to improve my writings here on steamit. Thank you very much. :DMay I have a favor? can you see my post "Tricks to find the square of a number"? Here is url https://steemit.com/math/@jhernel45/math-trick-finding-the-square-of-a-number.