Buongiorno a tutti cari amici, bentornati al primo "corso" di fisica su Steemit in Italiano. L'ultima volta ci siamo lasciati con la definizione di velocità media e qualche esempio teorico, per chi non lo avesse letto ecco qui il link alla prima lezione:
Immagine CC0 Creative Commons fonte

Oggi cominciamo con un esempio pratico di calcolo della velocità media, utilizzeremo due unità di misura del SI (sistema internzaionale) il metro per le lunghezze (m) e il secondo per il tempo (s):
Supponiamo che la legge oraria di un punto materiale che si muove sull'asse delle ascisse (l'asse x) sia:
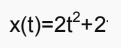
Vogliamo calcolare la velocità media del nostro punto tra gli istanti t1 = 0s e t2 = 4s, (dove s indica l'unità di misura presa in considerazione, in questo caso i secondi) come facciamo?
Abbiamo visto la volta scorsa che la velocità media è definita come il rapporto tra lo spazio percorso (∆x) e l'intervallo di tempo impiegato a percorrerlo (∆t), quindi ∆x / ∆t. Ma sappiamo che lo spazio percorso non è altro che la differenza tra il punto di arrivo (x2) e il punto di partenza (x1), e cosa sono x2 e x1? Sono i punti in cui si trova il nostro punto materiale in due diversi istanti dati rispettivamente dai tempi t2 e t1, quindi possiamo scrivere x2 e x1 come x(t2) e x(t1) (che si leggono: x nell'istante t2 e x nell'istante t1). Lo stesso ragionamento vale per l'intervallo di tempo (∆t), il quale è la differenza tra l'istante di arrivo (t2) e l'istante di partenza (t1), quindi t2 - t1
Allora la nostra differenza x2 - x1 diventa x(t2) - x(t1) che divisa per l'intervallo di tempo t2 - t1 ci fornisce la velocità media del punto materiale in quell'intervallo di tempo:
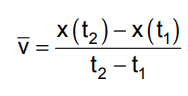
Ora che abbiamo scritto l'equazione risolutiva della velocità media possiamo procedere alla risoluzione matematica del problema:
Anzitutto sostituiamo la legge oraria data (x(t)) alle nostre x(t2) e x(t1), che diventano rispettivamente:
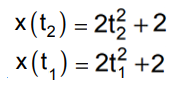
Riportandole quindi nell'equazione di partenza otteniamo:
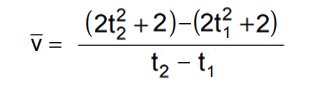
Togliamo le parentesi (ricordandoci di cambiare i segni nella seconda):
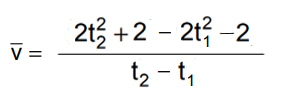
E dopo aver eliminato +2 e -2 (che si annullano) quello che rimane è:
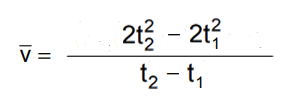
Ora andremo a sostituire t2 e t1 con gli istanti prescelti (t2=4 e t1=0):
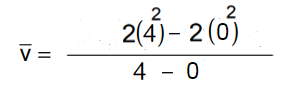
Da cui otteniamo che la velocità media del nostro punto materiale è pari ad 8 metri al secondo:
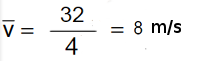
Se invece prendessimo l'intervallo compreso tra t1 = 1 e t2 = 3 avremmo un risultato diverso, che non vi dirò perchè ve lo lascio come esercizio ;) così potrete rendervi conto da soli che: generalmente la velocità media dipende dall'intervallo di tempo considerato.

Se consideriamo intervalli ∆t sempre piu’ piccoli, con t2 sempre piu’ vicino a t1, (quindi con il nostro intervallo di tempo ∆t sempre più vicino allo zero) arriviamo alla velocità istantanea. Essa è una grandezza che viene utilizzata per caratterizzare il moto dei corpi, per esempio il tachimetro della vostra automobile segna la velocità istantanea della vostra vettura.
Tuttavia, dal punto di vista algebrico, il rapporto ∆x / ∆t non è definito per ∆t = 0 (infatti non si può dividere per zero) per ovviare a questo problema e procedere con la definizione completa di velocità istantanea dobbiamo prima approfondire le nostre conoscenze matematiche introducendo i concetti di limite e derivata di una funzione:

Cominciamo considerando la seguente funzione:
.gif)
Essa è definita (è valida) per ogni valore di x diverso da 2, perchè se x fosse uguale a 2 cadremmo in una brutta situazione in cui avremmo 0/0 (che non è definito). In questo caso possiamo però riscrivere la funzione nel modo che segue (grazie alla differenza di quadrati):
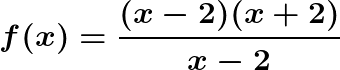.gif)
Da cui ricaviamo che la funzione (per x diverso da due) è uguale a:
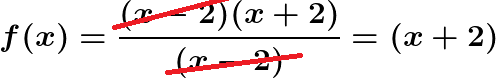
Vuol dire che più il valore di x si avvicina a 2, più il valore della funzione f(x) si avvicina a 4.
Per esempio se il valore di x fosse 1.8 il valore di f(x) sarebbe 1.8+2 = 3.8, mentre se ci avvicinassimo di più a 2, per esempio prendendo x = 1.999999 allora il valore di f(x) sarà di 3.999999.
.Per x che tende a 2 f(x) tende a 4
.Una funzione (come quella dell'esempio) può non essere definita in un punto X0 (nel nostro caso il punto X0 è 2), ma può avere un limite finito in quel punto.
Data una funzione f(x), definita su di un intervallo [a,b], si dice che la funzione ammette come limite L (L=numero finito, nel nostro caso L=4), quando x tende a x0, se:
.Preso un numero reale positivo ε (epsilon) arbitrariamente piccolo, è possibile determinare un numero positivo δ (delta) tale che:
.Per X compreso tra X0-δ e X0+δ (che avviene se e solo se il valore assoluto di X-X0 è minore di δ).
.Si ha che il valore assoluto di f(x)-L è minore di ε.
In formule:
.gif)
.gif)
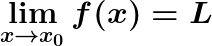.gif)
Si sembra una cosa difficilissima scritta così, e sotto certi aspetti lo è, ma noi prenderemo in esame esempi ed esercizi molto molto semplici, quanto basta per capire il concetto generale, per analizzare l'argomento in profondità infatti non credo che basterebbero 20 post. Per funzioni semplici, il limite si può calcolare applicando direttamente la definizione di cui sopra, mentre per funzioni più complicate si utilizzano alcuni teoremi sui limiti
(il link rimanda ad una pagina di matematicamente.it dove, per chi volesse approfondire, sono enunciati e dimostrati tutti i suddetti teoremi).
.gif)
Così a naso possiamo dire che se x tende a 2, il valore della funzione tenderà a 8, ma come facciamo ad esserne sicuri? Applichiamo la deifnizione di limite:
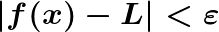.gif)
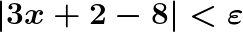.gif)
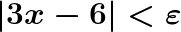.gif)
.gif)
.gif)
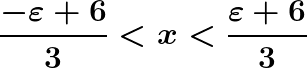.gif)
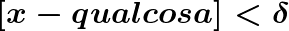.gif)
.gif)
.gif)
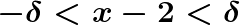.gif)
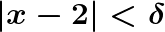.gif)
E il limite risulta verificato. Se volete fare pratica vi lascio un esercizio: provate a calcolare e verificare il seguente limite usando la definizione:
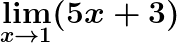.gif)
Focardi, Massa Uguzzoni: Fisica generale: Meccanica e termodinamica
A.Bacciotti, F. Ricci: Analisi matematica 1
Ero partito con l'idea di introdurre anche il concetto di derivata, ma ho visto che ore sono e devo andare a lavorare veloce come il vento, ma in ogni caso avrebbe preso troppo spazio, e avrebbe reso questo post ancora più pesante di quello che è. Quindi per il momento ci fermiamo qui, ci vediamo GIOVEDI' PROSSIMO per vedere cosa sono le derivate e approfondire il discorso sulla velocità istantanea. Fate gli esercizi mi raccomando ;)
A presto cari amici,


Being A SteemStem Member
sono arrivato a 4 m/s e poi ho sbattuto contro il muro :-) non ricordo piu i limiti :-)
This comment has received a 5.00 % upvote from @webdeals thanks @intronitro.
Bello @voghera! Bella idea ripassare un po’ di Fisica! Un saluto @giornalista
Grazie caro :)
Molto interessante, soprattutto la parte dei limiti.
Grazie @sciack, tu li vedrai fatti così tra qualche anno, ma puoi già portarti avanti e buttarci un occhio, prova a fare l'esercizio ;)
Qui mi sa che la mia testa non ci arriva subito🤔Ahah
Nessuno nasce "imparato" XD Questi sono argomenti che vanno assimilati piano piano ;)