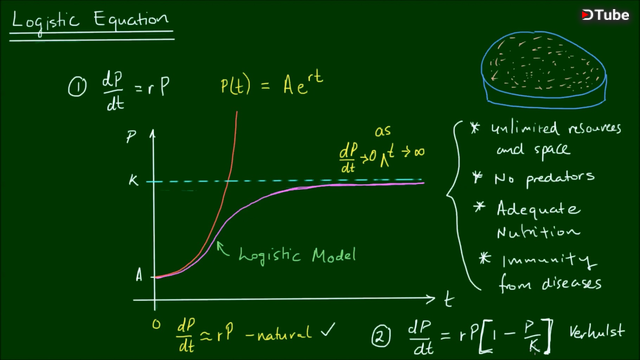
[DTube] The Logistic Differential Equation for Population Growth: General Solution

in #dtube • 6 years ago (edited)

In this video, we work through the process for deriving the analytical solution to the Logistic Equation formulated by Verhulst for modelling population growth.

We first compare the natural (exponential) and logistic models and their formulas.

The logistic equation is given by:

dP/dt = rP [1 - K/P]

This is a separable differential equation with which we can separate the variables and solve by integration.

First Order Differential Equation Videos

  1. Modelling the Decay of Nuclear Medicine with dy/dx = -ky
  2. Newton's Law of Cooling
  3. The Logistic Differential Equation for Population Growth: General Solution

Thanks for watching. Please give me a "thumbs up" if you have found this video helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

▶️ DTube
▶️ IPFS
#steemstem #teamaustralia #mathematics #calculus
6 years ago in #dtube by
$2.74
  • Past Payouts $2.74
  • - Author $2.10
  • - Curators & beneficiaries $0.64
  • > dtube: $0.14
332 votes
Reply 1
Sort:  
  • Trending
    • [-]
     6 years ago  




    This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.

    If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!

    For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!