Billions of neurons in our brain allow to perform thousands of operations per second. But, unlike the computer, we make not only mathematical calculations, we analyze information as a whole.
That is why we are often faced with the situation, when our intuitive calculations of statistics and probability become incorrect. Because of this, many things seem to us incredible, while in fact they are subject to the laws of mathematics.

One of my favorite tricks of statistics is Penney's Game ( nontransitive paradox). The most clear and simple example to explain the principle of this paradox- game "heads or tails".
The rules of the game “heads or tails”: 2 players, in the beginning each player must name the combination-a sequence of three tosses (heads-heads-tails, tails-tails-heads,etc.)
It may seem that the chance of winning of each player 50/50, and it is impossible to influence the probability of a correct combination. After all, according to the theory of probability: the result of current throw does not depend on the previous result.

In fact, if you make your move second (call your combination after another player), the probability of your winning will be 2/3 (87%).
- RULE 1 -Your first choice should be the opposite of the second choice of opponent.
- RULE 2 -Your second and third choice should match with first and second choice of opponent.
For example:
Your opponent first named his combination: head-head-tail.
Your combination will be: tail-head-head.Opponent’s combination: tail-head-tail.
Your combination: tail-tail-head.
In another words: First's player choice: "1- 2- 3", Second’s player choice: "not2- 1- 2"

Let’s try to simplify the understanding: tail is 0, head is 1. The first player chose a combination 000, then you should chose 100. The first player can win only in one case: if his combination will fall in the beginning, but the probability of this event is 1/8. The advantages of the second player is clear: he will win, once in a sequence of shots will appear 1.
How it works? The first player really can't affect the probability of winning (whatever combination he chose). While the second player actually sets the parameters of his victory, on the basis of the first combination.
Rule 1 breaks the combination of our enemy, in the middle of its implementation (now he needs at least two successful moves in a row to make it come true).
Rule 2, on the contrary, specifies a condition that the combination of the enemy begins to come true… while our sequence is already realized.
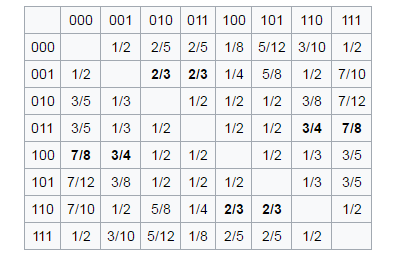
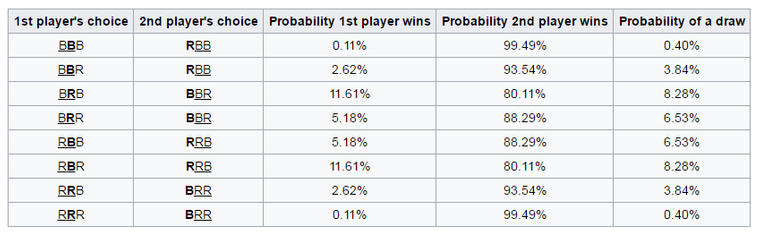
The essence of the paradox is that there is no “strongest” combination. For each combination there is always the option which will be “stronger”.

Our brain can't see the dependence of the probabilities, and their influence on each other. Because when calculating our brain uses not only the raw numbers and logic, it is also guided by life experience, intuition and guess-work. It is difficult to understand Penney's game, more difficult to imagine how works the rule "not2, 1, 2", even having example before your eyes. However, Penney's game is a reality.
sources: Penney's Game Wiki, Intransitivity, Magic of statistics images from Google Search.

Great post. Please follow @steemiteducation so that we can read more of your posts, and help you succeed.
Thank you so much! :)
This is a fantastic post!
i'm glad that you liked it. thank you for reading!
It is an interesting break down of a pretty mundane game! You could probably do something similar with rock, paper, scissors if you were so inclined!
You are right. It's even work witn D&D game :)
I even found information which describes a special game for the CIA, on the basis of Intransitivity.
Heads or tails is about my limit.
Really interesting... guess because I'm a nerd...a really sexy cool nerd. 😎
Resteemed!
upped
Thank you!
:)
Very interesting mathematics is obtained. Never thought about it. As it does not fit in my head, that it is possible.
Well, now you can play for money, with 87% probability to win :)